Game-Theoretic Autonomous Driving via Graphs of Convex Sets
A framework for solving autonomous driving problems using graphs of convex sets and iterative best response.
Disclaimer: Some of the content in this report might be inaccurate or incorrect. Please refer to the preprint version of this work for the most accurate information. The preprint can be found here
Overview
This was a final project report for the ASE 381P18 Game-Theoretic Modeling of Multi-Agent Systems course taught by Dr. David Fridovich-Keil at the University of Texas at Austin. For this project, we chose to solve autonomous driving problems using graphs of convex sets (GCS)
Motivation
Autonomous driving in mixed traffic is a complex “dance” between vehicles. Drivers must balance individual goals (getting to a destination quickly) with shared safety constraints (avoiding collisions). This paper introduces IBR-GCS (Iterative Best Response based on Graphs of Convex Sets), a framework that treats highway driving as a strategic game, combining discrete decision-making with continuous trajectory optimization.
The Core Challenge is a Hybrid Problem
Multi-vehicle planning is inherently hybrid because it involves two very different types of reasoning:
- Discrete Decisions: Should I stay in my lane, change left, or change right? (Combinatorial)
- Continuous Decisions: How much should I accelerate or steer to stay safe? (Numerical)
Traditional methods often struggle to scale these two together. IBR-GCS solves this by using the Graphs of Convex Sets (GCS) framework, which allows complex, non-convex environments to be modeled as a series of connected convex regions.
How the IBR-GCS Framework Works
The novelty of IBR-GCS lies in its vehicle-specific, strategy-dependent construction. Instead of one giant map, each vehicle builds its own “view” of the world based on what other cars are doing.
Building the Graph (Vertices & Edges)
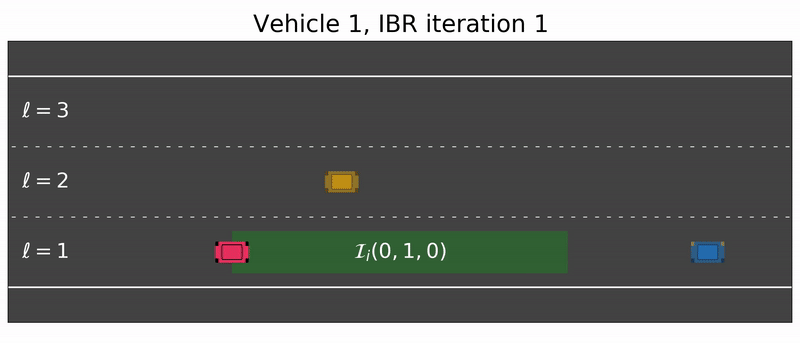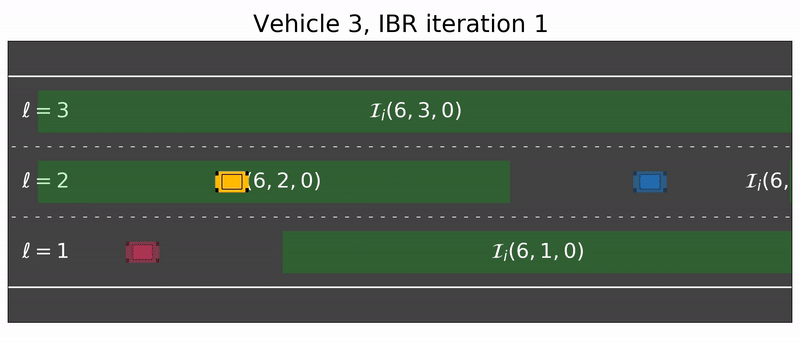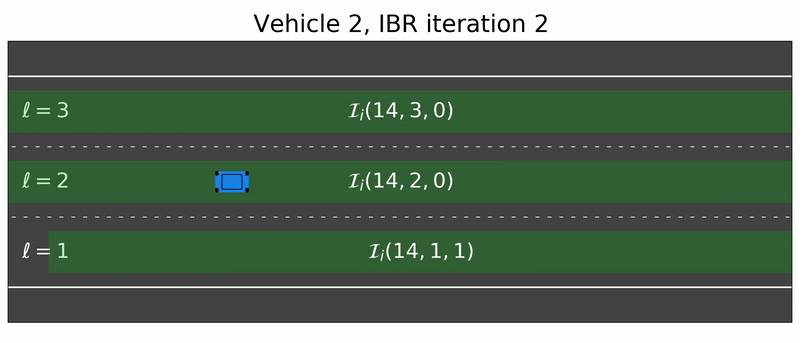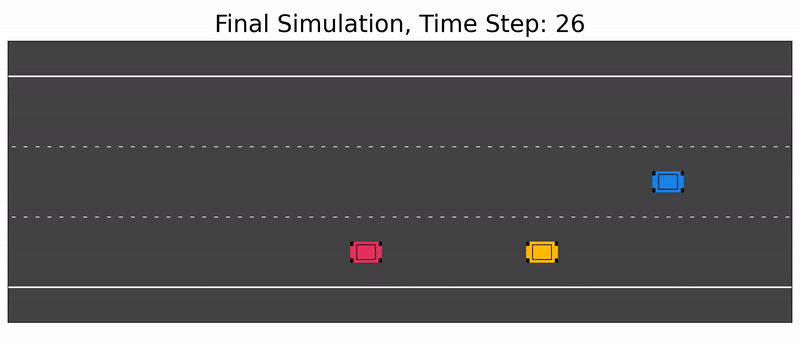
- Vertices (Safe Gaps): The algorithm identifies “safe gaps” in each lane. These are longitudinal intervals where a vehicle can exist without hitting another car. These gaps are modeled as convex sets.
- Edges (Transitions): These represent the “moves” between gaps. An edge encodes the physics of the car (acceleration limits) and ensures that lane changes follow traffic rules.
The Game Theory (Iterative Best Response)
Since one car’s “safe gap” depends on where the other cars are, the system uses Iterative Best Response (IBR).
- Step A: Vehicle 1 plans its best path while assuming others stay on their current paths.
- Step B: Vehicle 2 plans its best path, now accounting for Vehicle 1’s new plan.
- Step C: This repeats until the strategies stabilize into a Generalized Nash Equilibrium (GNE) which is a state where no driver can improve their situation without violating safety.
Potential Games
The paper identifies that this driving scenario can be modeled as a Generalized Potential Game. This means the incentives of all individual vehicles can be summarized by a single global Potential Function:
\[\Phi(\theta) = \sum_{i \in \mathcal{N}} J_i(\theta_i),\]where:
- $\Phi$ is the global potential.
- $J_i$ is the individual cost for vehicle $i$ (e.g., deviating from desired speed).
- $\theta_i$ is the chosen strategy (trajectory).
By showing that each vehicle’s “best response” reduces this potential function, we prove that the system will eventually converge to a safe, stable equilibrium.
Numerical Simulations
We implemented the IBR-GCS algorithm in Python and tested it on various autonomous driving scenarios, including lane changing and intersection crossing. The simulations demonstrated that the IBR-GCS algorithm can effectively generate safe and efficient trajectories for multiple autonomous vehicles in dynamic environments.