Covariance Steering via System Level Synthesis

Steering a team of agents with stochastic dynamics from an initial Gaussian distribution to a final one under communication delays.

Overview

This is a final project report for the ASE 389 Networked Control Systems course taught by Dr. Takashi Tanaka at the University of Texas at Austin. For this project, I chose to solve the finite-horizon covariance steering problem using system-level synthesis. As outlined throughout the report, there are a number open questions that are yet to be answered, and so this project is considered a work in progress and will be updated as more research is conducted.

Introduction

The motivation of this work is to unify two exciting areas of control theory, namely, covariance control and system-level synthesis . The main goal is to develop a distributed stabilizing controller to steer a team of agents from an initial Gaussian distribution to a final one under communication delays and stochastic linear dynamics. This was accomplished through the following three steps:

1. Formulate the covariance steering problem as a convex optimization problem using system responses.

2. Setup a partially nested information structure by sparsifying the system responses based on the delay structure graph.

3. Distribute the problem for a team of agents using the alternating direction method of multipliers (ADMM).

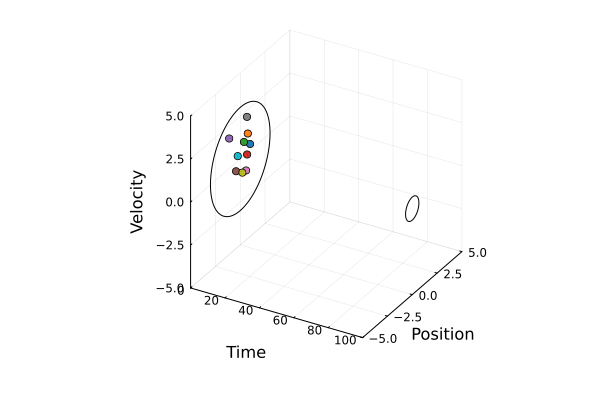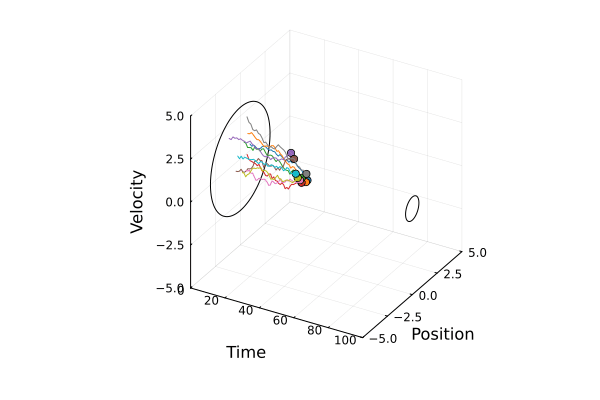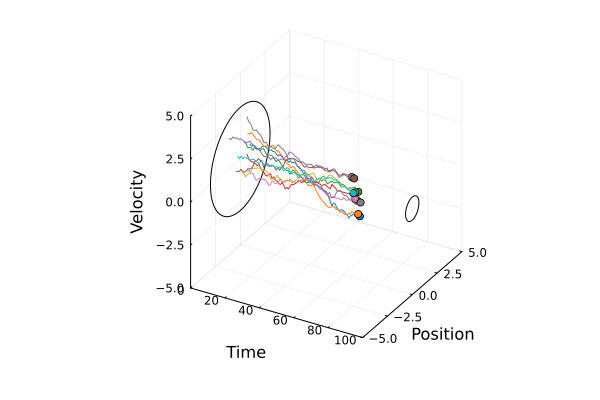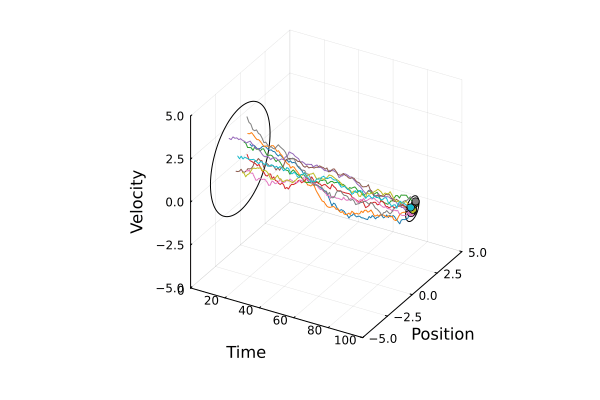
Problem Formulation

The optimal control problem that we seek to solve is given by: \(\begin{split} \minimize_{x_t, u_t} \quad& \sum_{t=0}^T \mbb{E} \left[x_t^\top Q_t x_t + u_t^\top R_t u_t \right] \\ \subjectto \quad& x_{t+1} = A_t x_t + B_t u_t +w_t,\\ &\mbb{E}[x_0] = \mu_0, && \mbb{E}[x_T] = \mu_f,\\ &\Sigma_0 = \Cov[x_0],&& \Sigma_f = \Cov[x_T], \label{eqn:finalcovarianceconstraint} \end{split}\)

where \(x_t \in \mbb{R}^n\) is the state, \(u_t \in \mbb{R}^m\) is the control input, and \(w_t \in \mbb{R}^n\) is a disturbance process such that \(w_t \overset{\textbf{i.i.d.}}{\sim} \mathcal{N}(\mu_w = 0, \Sigma_w)\). \(A_t \in \mbb{R}^{n \times n}\) and \(B_t \in \mbb{R}^{n \times m}\) are discrete matrix functions for the state and control input, respectively. \(Q_t \in \mbb{S}^{n}_{+}\) and \(R_t \in \mbb{S}^{m}_{++}\) are weighting matrices on the state and control input, respectively.

Open question: What if $\mu_w \neq 0$?

System Level Synthesis

The discrete stochastic linear-time-varying (LTV) system, \begin{equation} x_{t+1} = A_t x_t + B_t u_t + w_t, \end{equation} can be written in the following matrix form:

\[\begin{bmatrix} x_0 \\ x_1 \\ \vdots \\ x_T \end{bmatrix} = \begin{bmatrix} 0 \\ A_0 & 0 \\ & A_1 & 0 \\ & & \ddots & \ddots \\ & & & A_{T-1} & 0 \end{bmatrix} \begin{bmatrix} x_0 \\ x_1 \\ \vdots \\ x_T \end{bmatrix} + \begin{bmatrix} 0 \\ B_0 & 0 \\ & B_1 & 0 \\ & & \ddots & \ddots \\ & & & B_{T-1} & 0 \end{bmatrix} \begin{bmatrix} u_0 \\ u_1 \\ \vdots \\ u_T \end{bmatrix} + \begin{bmatrix} x_0 \\ w_0 \\ w_1 \\ \vdots \\ w_{T-1} \end{bmatrix}.\]

Introducing the following signals and block-lower-triangular matrices:

\(\mbf{x} = \begin{bmatrix} x_0 \\ x_1 \\ \vdots \\ x_T \end{bmatrix}, \mbf{u} = \begin{bmatrix} u_0 \\ u_1 \\ \vdots \\ u_T \end{bmatrix}, \mbf{w} = \begin{bmatrix} x_0 \\ w_0 \\ w_1 \\ \vdots \\ w_{T-1} \end{bmatrix}, \mbf{K} = \begin{bmatrix} K^{0,0} \\ K^{1,1} & K^{1,0} \\ \vdots & \ddots & \ddots \\ K^{T,T} & \cdots & K^{T,1} & K^{T,0} \end{bmatrix}, \mcl{Z} \coloneqq \begin{bmatrix} 0 \\ I & 0 \\ & I & 0 \\ & & \ddots & \ddots \\ & & & I & 0 \end{bmatrix},\) \(\mcl{A} \coloneqq \blkdiag (A_0, A_1, \dots, A_{T-1}, 0)\), and \(\mcl{B} \coloneqq \blkdiag (B_0, B_1, \dots, B_{T-1}, 0)\). The variable \(\mbf{K}\) is the matrix representation of the convolution operator induced by the linear-time-varying controller \(K_t\) such that \(u_t = \mbf{K}^{t,*} \mbf{x}\), for \(\mbf{K}^{t,*}\) the \(t\)-th row of \(\mbf{K}\).

The discrete stochastic linear-time-varying (LTV) system can then be written as:

\[\begin{split} \mbf{x} &= \mcl{Z} \left(\mcl{A} \mbf{x} + \mcl{B} \mbf{u} \right) + \mbf{w} \\ &= \mcl{Z} \left(\mcl{A} \mbf{x} + \mcl{B} \mbf{K x} \right) + \mbf{w} \\ &= \mcl{Z} \left(\mcl{A} + \mcl{B} \mbf{K} \right) \mbf{x} + \mbf{w}. \end{split}\]

In particular, the closed-loop behavior of the system under the feedback law $\mbf{K}$ can be entirely characterized by the following maps,

\[\begin{split} \mbf{x} &= \left(I - \mcl{Z} \left( \mcl{A} + \mcl{B} \mbf{K} \right) \right)^{-1} \mbf{w} \\ \mbf{u} &= \mbf{K} \left(I - \mcl{Z} \left( \mcl{A} + \mcl{B} \mbf{K} \right) \right)^{-1} \mbf{w}, \end{split}\]

which describe the closed loop transfer functions from the disturbance \(\mbf{w}\) to the state \(\mbf{x}\) and control input \(\mbf{u}\), respectively. These maps are called system responses.

Introducing two additional lower-block-triangular operators,

\[\boldsymbol{\Phi}_x = \begin{bmatrix} \Phi_x^{0,0} \\ \Phi_x^{1,1} & \Phi_x^{1,0} \\ \vdots & \ddots & \ddots \\ \Phi_x^{T,T} & \cdots & \Phi_x^{T,1} & \Phi_x^{T,0} \end{bmatrix}, \boldsymbol{\Phi}_u = \begin{bmatrix} \Phi_u^{0,0} \\ \Phi_u^{1,1} & \Phi_u^{1,0} \\ \vdots & \ddots & \ddots \\ \Phi_u^{T,T} & \cdots & \Phi_u^{T,1} & \Phi_u^{T,0} \end{bmatrix}.\]

Here \(\boldsymbol{\Phi}_x\) denotes the system response describing the map from \(\mbf{w} \mapsto \mbf{x}\), and similarly, \(\boldsymbol{\Phi}_u\) to denote the system response describing the map from \(\mbf{w} \mapsto \mbf{u}\), thus

\[\begin{bmatrix} \mbf{x} \\ \mbf{u} \end{bmatrix} = \begin{bmatrix} \boldsymbol{\Phi}_x \\ \boldsymbol{\Phi}_u \end{bmatrix} \mbf{w}.\]

Instead of optimizing over the controller map \(\mbf{K}\), the optimal controller synthesis can be performed by optimizing over the pair of system responses \(\{\boldsymbol{\Phi}_x, \boldsymbol{\Phi}_u \}\). Note that \(\Phi_x^{t,0} = I, ~ \forall t \in [0, T]\).

Formulation using System Responses

Using vector notation, the problem can be written as:

\[\begin{split} \minimize \limits_{\mbf{x}, \mbf{u}} \quad& \left\Vert \begin{bmatrix} \mcl{Q}^{1/2} & 0 \\ 0 & \mcl{R}^{1/2} \end{bmatrix} \begin{bmatrix} \mbf{x} \\ \mbf{u} \end{bmatrix} \right\Vert_F^2 \\ \subjectto \quad& \mbf{x} = \mcl{Z A} \mbf{x} + \mcl{Z B} \mbf{u}, \\ &\mbb{E}[\mcl{P}_0 \mbf{x}] = \mu_0, && \mbb{E}[\mcl{P}_T \mbf{x}] = \mu_f, \\ &\Sigma_0 = \Cov[\mcl{P}_0 \mbf{x}], && \Sigma_f = \Cov[\mcl{P}_T \mbf{x}], \end{split}\]

where \(\mcl{Q} \coloneqq \blkdiag (Q_0, Q_1, \dots, Q_T),~ \mcl{R} \coloneqq \blkdiag (R_0, R_1, \dots, R_T),\) and \(\mcl{P}_i\) is a block matrix with zero blocks everywhere except with an identity block in at the index \(i,i\).

However, using the state system response \(\mbf{x} = \boldsymbol{\Phi}_x \mbf{w}\):

\[\begin{split} \Cov[\mcl{P}_i\mbf{x}] &= \mcl{P}_i\mbf{x} \mbf{x}^\top \mcl{P}_i^\top \\ &= \mcl{P}_i \boldsymbol{\Phi}_x \mbf{w} \mbf{w}^\top \boldsymbol{\Phi}_x^\top \mcl{P}_i^\top\\ &= \mcl{P}_i \boldsymbol{\Phi}_x \Sigma_w \boldsymbol{\Phi}_x^\top \mcl{P}_i^\top. \end{split}\]

Using \(\mbf{x} = \boldsymbol{\Phi}_x \mbf{w}\) and \(\mbf{u} = \boldsymbol{\Phi}_u \mbf{w}\) to cast the problem as an optimization over system responses:

\[\begin{split} \minimize \limits_{\boldsymbol{\Phi}_x, \boldsymbol{\Phi}_u} \quad& \left\Vert \begin{bmatrix} \mcl{Q}^{1/2} & 0 \\ 0 & \mcl{R}^{1/2} \end{bmatrix} \begin{bmatrix} \boldsymbol{\Phi}_x \\ \boldsymbol{\Phi}_u \end{bmatrix} \Sigma_w^{1/2} \right\Vert_F^2 \\ \subjectto \quad& \begin{bmatrix} I-\mcl{Z A} & -\mcl{Z B} \end{bmatrix} \begin{bmatrix} \boldsymbol{\Phi}_x \\ \boldsymbol{\Phi}_u \end{bmatrix} = I, \\ &\mcl{P}_0 \boldsymbol{\Phi}_x \mu_w = \mu_0, &&\mcl{P}_T \boldsymbol{\Phi}_x \mu_w = \mu_f, \\ &\Sigma_0 = \mcl{P}_0 \boldsymbol{\Phi}_x \Sigma_w \boldsymbol{\Phi}_x^\top \mcl{P}_0^\top, && \Sigma_f = \mcl{P}_T \boldsymbol{\Phi}_x \Sigma_w \boldsymbol{\Phi}_x^\top \mcl{P}_T^\top. \end{split}\]

This problem has a convex quadratic cost function and affine constraints for the dynamics and mean boundary conditions. The two covariance boundary conditions are problematic due to their non-convexity.

Convexification of Covariance Constraints

The covariance constraints \(\Sigma_i = \mcl{P}_i \boldsymbol{\Phi}_x \Sigma_w \boldsymbol{\Phi}_x^\top \mcl{P}_i^\top\) can be relaxed by replacing the equality with an inequality ,

\[\begin{split} \Sigma_i \succeq \mcl{P}_i \boldsymbol{\Phi}_x \Sigma_w \boldsymbol{\Phi}_x^\top \mcl{P}_i^\top, \end{split}\]

which is convex and can be written as the following semi-definite constraint,

\[\begin{split} \begin{bmatrix} \Sigma_i & \mcl{P}_i \boldsymbol{\Phi}_x \Sigma_w^{1/2} \\ \left(\mcl{P}_i \boldsymbol{\Phi}_x \Sigma_w^{1/2}\right)^\top & I \end{bmatrix} \succeq 0, \end{split}\]

using the Schur complement.

Open question: When is this constraint tight?

Complete Convex Optimization Problem

The complete convex covariance steering problem using system responses is given by,

\[\begin{split} \minimize \limits_{\boldsymbol{\Phi}_x, \boldsymbol{\Phi}_u} \quad& \left\Vert \begin{bmatrix} \mcl{Q}^{1/2} & 0 \\ 0 & \mcl{R}^{1/2} \end{bmatrix} \begin{bmatrix} \boldsymbol{\Phi}_x \\ \boldsymbol{\Phi}_u \end{bmatrix} \Sigma_w^{1/2} \right\Vert_F^2 \\ \subjectto \quad& \begin{bmatrix} I-\mcl{Z A} & -\mcl{Z B} \end{bmatrix} \begin{bmatrix} \boldsymbol{\Phi}_x \\ \boldsymbol{\Phi}_u \end{bmatrix} = I, \\ & \begin{bmatrix} \mcl{P}_0 \\ \mcl{P}_T \end{bmatrix} \boldsymbol{\Phi}_x \mu_w = \begin{bmatrix} \mu_0 \\ \mu_f \end{bmatrix},\\ &\begin{bmatrix} \boldsymbol{\Sigma} & \mcl{P} \boldsymbol{\Phi}_x \Sigma_w^{1/2} \\ \left(\mcl{P} \boldsymbol{\Phi}_x \Sigma_w^{1/2}\right)^\top & I \end{bmatrix} \succeq 0, \end{split}\]

where \(\boldsymbol{\Sigma} = \begin{bmatrix} \Sigma_0 \\ \Sigma_F \end{bmatrix}\) and \(\boldsymbol{\mcl{P}} = \begin{bmatrix} \mcl{P}_0 \\ \mcl{P}_T \end{bmatrix}.\)

This problem can now be solved using an off-the-shelf convex optimization solver! CXYPY is used in this work.

CVXPY Implementation

Comparison with Other Parametrizations

There exist a number of parametrizations that are used in the literature to solve the covariance steering problem. The following table provides a comparison between the parametrization used in this work and other parametrizations used in the literature.

This Parametrization	Other Parametrizations
1: \(\mcl{Q}\)	1: \(\boldsymbol{\Phi}\)	11: \(\mcl{Q}\)
2: \(\mcl{R}\)	2: \(\mbf{K}\)	12: \(\mcl{R}\)
3: \(\mcl{Z}\)	3: \(\mbf{Z}\)	13: \(\mbf{H}\)
4: \(\mcl{A}\)	4: \(\mcl{P}_N\)	14: \(\mbf{G}\)
5: \(\mcl{B}\)	5: \(\boldsymbol{\Psi}, \Psi\)	15: \(\boldsymbol{\Gamma}\)
6: \(\boldsymbol{\Phi}_x\)	6: \(\mcl{X}_w\)	16: \(\mbf{F}, \phi\)
7: \(\boldsymbol{\Phi}_u\)	7: \(\mcl{X}_0\)	17: \(\mbf{X}_w = (\mbf{I} - \mbf{HF})^{-1} \mbf{G}\)
8: \(\mcl{P}_0\)	8: \(\mcl{U}_w\)	18: \(\mbf{X}_0 = (\mbf{I} - \mbf{HF})^{-1}\)
9: \(\mcl{P}_T\)	9: \(\mcl{U}_0\)	19: \(\mbf{U}_w = F(\mbf{I} - \mbf{HF})^{-1}\mbf{G}\)
10: \(\mbf{K} = \Phi_u \Phi_x^{-1}\)	10: \(\mathfrak{J}\), \(\mbf{f}\)	20: \(\mbf{U}_0 = F(\mbf{I} - \mbf{HF})^{-1}\)

It is important to note that this parametrization uses roughly half the number of variables compared to other parametrizations, making it more elegant and succinct. However, more importantly, this parametrization is more computationally efficient, since it doesn’t require the inversion and multiplication of many matrices, as in other parametrizations.

Open question: Which parametrization is more computationally efficient?